Автоматизация

[tarnyagin]

-- Девочки, вы, конечно, всё красиво нарисовали, но утверждать что "данные стремятся к нормальному t-распределению" -- это немножко голословно. В общем, так: переделайте мне их в гистограммы и наложите поверх соответствующую гауссовую кривую. Ладно? Ну вот и договорились :)



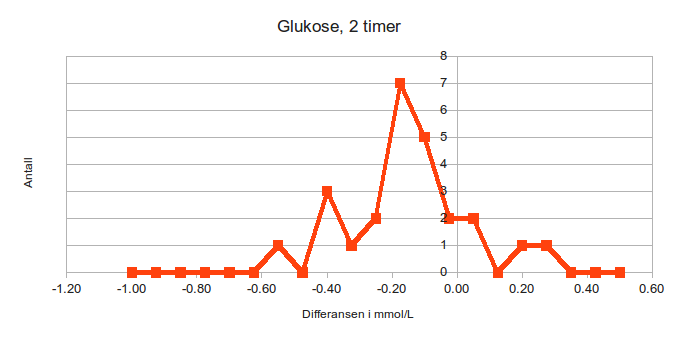
Девочки (Наташка с Рутой) разве не в слезах ушли. Во-первых графиков тридцать. Во вторых -- а как в excel наложить на график гауссиану? Точнее, даже не в excel (там есть для этого платный плагин), а в libreoffice?

Переделать график в гистограмму -- просто, хоть и трудоёмко. Про это я не буду, примем как данность промежуточный результат.


А вот наложить поверх рисунок -- засада. Никак. Из инструментов у libreoffice есть только кривые Безье. Вы пробовали нарисовать гауссов колокольчик мышкой от руки? Хорошо, что есть калькулятор:

#!/usr/bin/calc -p -f
#

dryrun = 0;
maxx = 570;
maxy = 400;
off = 0.075;
left = -1 - off/2;
right = 0.5 + off/2;
mu = -0.19;
sigma = 0.189;
dx = 4;

define g(x) = 1 / (sigma * sqrt(2 * pi())) * exp(-1/2 * ((x - mu) / sigma) ^ 2);

curr_y = round(g(left) * maxy * sigma);

system(strprintf("xdotool mousemove_relative -- %d %d", 0, -curr_y));

if (!dryrun) {
  system("xdotool mousedown 1");

  for(x = 0; x < maxx; x += dx) {
    xx = (x / maxx) * (right - left) + left;
    y = round(g(xx) * maxy * sigma);
    dy = curr_y - y;
    curr_y = y;

    system(strprintf("xdotool mousemove_relative -- %d %d", dx, dy));
  }
  system("xdotool mouseup 1");
  system("xdotool click 3");
  system("xdotool key i");
}

printf("Top at %.3f\n", 25 * g(mu) * off);

Ключ к решению, конечно, xdotool. Скрипт запускается с задержкой в семь секунд, за это время надо переключится в окно либр-калка, выбрать диаграммку, схватить в руки кривую Безье (типа карандаш) и ждать. А дальше включается в работу скрипт, нажимает мышку, ведёт её недрогнувшей рукой и отпускает. :). Вот что получилось:

Comments

Рекомендации бывалых

[dimview]

Во-первых, вместо гистограмм рисовать функции распределения (Empirical Cumulative Distribution Function, ECDF).

Во-вторых, нормальное распределение можно легко приблизить косинусом в большой степени.

В-третьих, проводить проверку на нормальность лучше не на глаз, а с помощью теста Колмогорова-Смирнова, который сравнивает те самые CDF. К сожалению, как и все тесты на нормальность, он измеряет размер выборки, поэтому практического значения не имеет.

Ну и в-четвёртых, R Studio и R Markdown для таких дел - отличное подспорье.

Re: Рекомендации бывалых

[skittishfox]

В-третьих, тест на нормальность красивей всего показывать в виде Q-Q Plot, а Колмогоров-Смирнов - это оверкилл.

Можно и так

[dimview]

Но Q-Q plot гораздо сложнее объяснить человеку, который с ним раньше не встречался, чем CDF.

Колмогоров-Смирнов как раз понятнее - можно даже стрелочку нарисовать в том месте, где максимум разницы между ECDF и теоретической функцией распределения и показать на неё пальцем, а не просто тыкать в загадочный p-value.

Re: Рекомендации бывалых

[tarnyagin]

Спасибо! :)

Они бакалавры, такого не умеют, хотя ECDF я могу попробовать объяснить. Тут, видишь, какая еще беда: нормальность распределения для некоторых аналитов доовольно сомнительная, и по-хорошему надо непараметрические тесты применять, Wilcoxon и прочие, но это, во первых, далекоооо за границей пройденного, во вторых не дает возможности сравнить уход величин с клинически значимыми порогами, то есть ломает всю идею диплома. Забивать лишний гвоздь Колмогоровым не хочется :). У них и так будет что-то вроде "мы видим, что данные не вполне нормальны, но если бы они были такими, то..."

Так это

[dimview]

Колмогоров-Смирнов как раз непараметрический.

Но идея тут не в этом. Я вот ни разу не видел в реальных данных нормального распределения. Оно всегда какое-то ненормальное. Вопрос только в размере выборки. На тех выборках, которые можно набрать руками в табличку, никакие тесты на нормальность ненормальность не покажут. Но:

1. Это не значит, что данные нормально распределены и

2. Даже если данные не распределены нормально, модель скорее всего всё равно можно использовать, и она будет хорошо работать.